[ 2014-July-17 13:17 ]
Vector clocks are a way of representing the partial order of events in a distributed or concurrent system. They allow you to compare two events
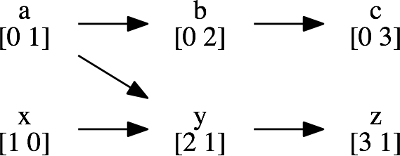
Consider two independent threads (T1 and T2) that both perform three operations (a, b, c and x, y, z). On each thread, I know the operations are in their program order (e.g. T1: a → b → c and T2: x → y → z). However, I can't say anything about the relative order of the events between the threads (e.g. a and z could happen in any order). However, if there is some sort of synchronization, then I can reason about the order. For example, consider that T1's first operation is actually sending a message, and T2's second operation is receiving that message. In this case, I know that T2's remaining events must happen after T1 sends the message. Here is a diagram which helps make this clear:
My first attempt to automatically generate these diagrams was not very helpful. I compared each event to every other event, and outputted an edge if one happens before the other. This results in far too many edges:
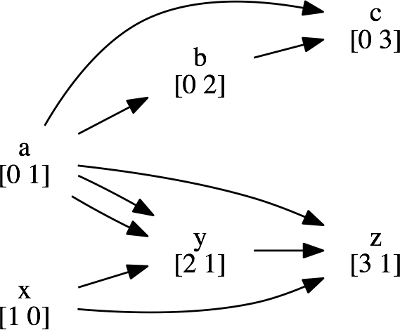
This is more cluttered and doesn't add any additional information, so I needed to remove these excess edges. The idea is to remove the edges that are implied by transitivity. In other words: if a → b and b → c, then I can infer that a → c, so I don't need that edge. It turns out that this is called transitive reduction, and graphviz includes a program called tred to do it. However, I need this information anyway. These events that happen "immediately before" are the ones I need to examine with my model checker, in order to determine if the correct result was produced. Calling this "transitive reduction" makes it sound complicated, but if you don't care about efficiency it isn't that hard:
First, for a given clock (c), find all events that happen before this one by comparing it with with every other clock. In this "before" set, remove any event (x) that happens before another one (y), because that means there is a transitive relationship (x → y → c). This requires comparing each node in the before set with every other node in the before set, which is worst case O(n2). Finally, any remaining nodes in this set are the events are "immediately" before this clock, so add edges to connect them.
I believe this is a worst case O(n3) algorithm, which I expected to be far worse than the best. However, Wikipedia claims the best known algorithm for transitive reduction is O(n2.3727), or O(nm) where m is the number of edges. Since the worst case number of edges is O(n2), this appears to be not a terrible way to do this.